Is Vandermonde aspirin for Cognitive headaches?

In a previous PolicyTracker blog post (DIDO, the Shannon Law, and an antenna for every citizen), I discussed the idea that using a vast number of distributed antennas (eg one for every citizen) could enable the spectrum to be used many times over, effectively permitting each user access to all the spectrum, all the time.

Whilst the cost and implementation of such a scheme would be as vast as the number of antennas involved, a more practical approach to re-using the same spectrum for multiple users has recently been proposed by the Alcatel-Lucent chair on Flexible radio, at
Supelec, France (Vandermonde frequency division multiplexing for cognitive radio).  The idea is named after French mathematician Alexandre-Théophile Vandermonde, not because of a re-discovery of some long lost mathematical process, but for his work on linear algebra, and in particular the Vandermonde matrix.  More of this later.

The concept is, that for any given user, there is a defined set of frequency-domain paths from every transmitter that is close enough to provide a signal.  Those paths can be modelled as a set of frequency dependent path profile co-efficients (lost you yet?)  If you know the path profile from a wanted transmitter to the user it is serving, and you know the path profile from any unwanted transmitter to that same user, it is possible to calculate a set of frequencies that can be transmitted from the unwanted transmitter that will not cause interference to that from the wanted transmitter.

Let’s take an example, say the path from a wanted transmitter to a user had a frequency profile that looked like the blue line in the graph below, and the path from  an interfering transmitter to that same user had a profile that looked like the orange line. For a received signal to be strong enough to be used by the user, it must be of a strength over the dotted green line.

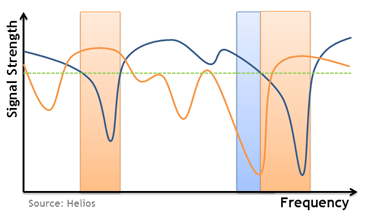
There are two areas of spectrum (those highlighted in orange) where the wanted signal is too weak (ie below the green line) to be able to provide the user with a service, and hence this spectrum could be used by the ‘orange’ transmitter with impunity, knowing that it would not cause additional interference to the user’s service, regardless of how strong its signal was.

There is a further area, shaded blue, in which the signals from the orange transmitter are sufficiently below the wanted signal from the ‘blue’ transmitter that they would also not cause interference.

Thus, some of the spectrum could be re-used to provide a service from the orange transmitter to a different user, without causing interference to the service from the blue transmitter. The path profiles would be different for each user, and would have to be calculated frequently, especially if users are highly mobile.  If the users were fixed (such as is the case for television receivers for example), the situation becomes much more straightforward.

The part that Vandermonde’s matrices play, is providing a mathematical mechanism for taking the different path profiles and working out which frequencies can be re-used by a potentially interfering transmitter.  The resulting concept has been termed ‘Vandermonde Frequency Division Multiplexing’ (VFDM) and is being proposed as a means of re-using spectrum on a cognitive basis.  As with the distributed antenna concept, it requires a lot of maths in both receivers and transmitters, but maths is, after all, what microprocessors are best at.

Whether VFDM, or for that matter distributed antennas, become reality is, perhaps, not the real story.  The fact that people are looking at extreme methods of frequency re-use in order to overcome the squeeze on spectrum availability perhaps reflects the headaches caused by their experiences of regulatory lethargy.  The cost of implementing such complex techniques clearly has to be counterbalanced with the stiction of some spectrum users to find means to become more spectrally efficient themselves.  Surely it is more cost effective to find a means to reduce the spectrum used for, for example, radars, than to introduce VFDM and the like into wireless networks.  Or maybe Vandermonde provides a means to use the spectrum allocated to more unwieldy users in a mathematically safe way, providing aspirin both for wireless networks clamoring to provide more capacity, and for those users sitting on spectrum which they are unwilling or unable to share without being guaranteed protection from interference.

P.S. Perhaps the time is right for an English mathematician to have their theories transposed into spectrum engineering for a change. I propose more research into the use of the Womersley number, named after my namesake John Womersley, to solve some currently undiscovered wireless viscosity problem!